Introducción
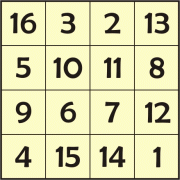
El cuadrado mágico de Durero es esto:
Y cumple las siguientes condiciones:
O sea suman 34 todas las filas, todas las columnas y todas las diagonales.
16+3+2+13=34
5+10+11+8=34
9+6+7+12=34
4+15+14+1=34
16+5+9+4=34
3+10+6+15=34
2+11+7+14=34
13+8+12+1=34
16+10+7+1=34
13+11+6+4=34
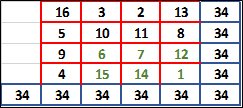
Además hay otra serie de sumas notables.
El cuadrado central también suma 34
10+11+6+7=34
Las cuatro esquinas suman 34
16+13+4+1=34
Las celdas de los extremos diagonales del cuadrado externo y del cuadrado interno suman 17 que es la mitad de 34.
16+1=17
13+4=17
10+7=17
11+6=17
Luego tenemos un total de 16 sumas.
Podemos definir “cuadrado mágico tipo Durero” a todo conjunto de 16 números enteros que cumplan con las 16 sumas explicadas.
Podemos definir el problema de Durero como aquel que pretende encontrar todos los cuadrados mágicos de Durero que existan.
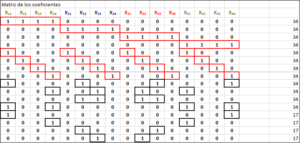
Entonces para hallar esos conjuntos de 16 números, utilizaremos las condiciones que deben de cumplir y que se enumeraron mas arriba. Si expresamos esas condiciones en forma de ecuaciones nos sale un sistema de 16 ecuaciones lineales con 16 incógnitas:
Y ahora se trata de resolver este sistema.
Si intentáis hacerlo a mano seguramente os vais a equivocar y tardaréis al menos un par de horas. Si se comete un error durante el cálculo, se arrastra y luego puede ser un quebradero de cabeza ver que no cuadran los resultados e intentar buscar el error.
Se impone pues resolverlo con ayuda del ordenador que para eso están. Estuve buscando una herramienta buena para esto y la mejor que encontré ha sido la web:
Matrixcalc.org
Me parece una web excepcional para todo lo que suponga calculo con matrices. Además puede hacer cálculos simbólicos, y así resolver también el problema parametrizando el término independiente.
El que tenga interés en ver la solución paso a paso del sistema de ecuaciones, lo puede consultar en el documento:
https://home.mycloud.com/action/share/d6783f1f-b962-4bdb-a7ef-b5d652f953fc
Interpretación y análisis de la solución
El vector solución general del sistema de 16 ecuaciones con 16 incógnitas para el caso particular y concreto del cuadrado mágico de Durero que el ideó en el s.XVI es:
El vector solución para el caso general con término independiente parametrizado es:
Observamos lo siguiente:
- Los coeficientes de la matriz principal, la matriz de los coeficientes, han de ser siempre los mismos, porque eso es lo que caracteriza a los cuadrados mágicos de Durero. Los criterios por los cuales hemos planteado el sistema de ecuaciones.
- Sin embargo, los términos independientes no tienen por qué ser:
(34, 34, 34, 34, 34, 34, 34, 34, 34, 34, 34, 34, 17, 17, 17, 17)
Si no que en general serán:
(a, b, c, d, e, f, g, h, u, j, k, l, m, n, w, p)
Fijaros que donde debía estar la “o” he puesto una w, y donde debía estar la “i” he puesto una u. Esto no es casual. Dependiendo de la tipografía usada, la web que resuelve el sistema puede no hacer bien los cálculos. Con estas combinaciones de letras no falla. Es posible que se haga un lío con el punto de la i a la hora de renderizar las imágenes.
- Finalmente, con estos parámetros la url que hace el cálculo directamente y que podéis utilizar directamente en vuestro navegador es:
Vemos entonces que los valores numéricos del vector solución que se dieron para el cuadrado mágico original de Durero, ahora pueden calcularse en función de los 16 componentes del término independiente:
(a, b, c, d, e, f, g, h, u, j, k, l, m, n, w, p)
Hasta aquí todo bien. Pero observemos una cosa. El sistema no tiene una solución única, sino muchas. De hecho infinitas si hacemos variar el vector término independiente.
El sistema tiene en efecto, 6 grados de libertad que de la solución dada han ido a parar a las variables:
x10, x11, x12, x14, x15, x16
Si damos valores arbitrarios a estas variables, calculando en cada caso que coeficientes les corresponden, tendremos un montón de conjuntos de 16 números que constituyen cuadrados mágicos de Durero.
Para simplificar el cálculo, vamos a acotar el problema.
- Solo vamos a considerar soluciones cuyos 16 valores sean estrictamente mayores que cero.
- Solo vamos a hacer variar los 6 grados de libertad entre 1 y 9
Evidentemente si consideramos el 0 y permitimos números negativos salen muchas soluciones mas, pero Durero nunca habría contemplado estos números para expresar el simbolismo que el quería y su relación con el misterio que pronto veremos.
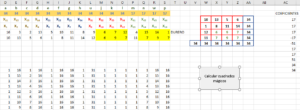
Para resolver este problema, he creado una hoja de cálculo Excel que nos permite visualizar como se construyen las soluciones.
El término independiente se puede cambiar simplemente introduciendo un número par en la columna D, donde ahora se ve un 34.
Después pulsamos el botón “calcular cuadrados mágicos” y el sistema irá escribiendo en sucesivas filas a partir de la celdilla D50 todas las soluciones posibles con las premisas expresadas mas arriba, haciendo variar los 6 grados de libertad (en amarillo).
Esta hoja de cálculo, junto con todos los archivos del proyecto se pueden descargar de:
https://home.mycloud.com/action/share/77e97160-4a74-4ee2-927d-efb77398ec13
También he desarrollado una base de datos que hace los mismos cálculos pero mas rápido y con mayor capacidad de almacenamiento:
Solo hay que pulsar el botón calcular cuadrados mágicos y calculará todos los cuadrados mágicos que almacenará en la tabla “CUADRADOS”.
Relación con el misterio
Hace unos días tuve la ocasión de de asistir a una conferencia en Madrid impartida por Josep Guijarro donde hablaba del conocido clásico del misterio de las serendipias o casualidades imposibles.
La tesis de Josep era: nacemos en un momento dado del tiempo y morimos entro momento mas adelante en el futuro. Unos mas adelante que otros. A lo largo de nuestra vida nuestra línea de tiempo va serpenteando, deslizándose a un lado y a otro y quizá, eventualmente, apartándose demasiado del recto camino.
Las serendipias o casualidades imposibles, vendrían a ser como los avisos que te da el universo para recentrarte. Ojo que estos avisos pueden ir acompañados de verdaderas contrariedades o golpes de mala suerte.
Yo creo que nuestro destino de alguna manera está escrito en ciertas combinaciones de números. Esto mismo creía Isaac Newton y es la base de la cábala o del estudio numerológico de la Biblia.
También apoya esta tesis el que se repita demasiado una fecha o grupos de fechas para determinados acontecimientos entre miembros de una familia. La metagenealogía se basa en esto. Jodorowsky y Jung creían en estas cuestiones, al igual que los sabios del renacimiento como Durero. Los cuadrados mágicos como el SATOR o el de Durero eran la manera que tenían los antiguos de introducirse en estos misterios.