INTRODUCCIÓN
Muchos de los seguidores de esta web de misterio, oyen los posts a través del podcast asociado en ivoox, del mismo nombre: La cripta de John Dee. Es una forma cómoda de oírlo porque se puede hacer otra cosa mientras. No obstante yo recomiendo para una mejor experiencia el uso de unos buenos cascos con supresión de ruido ambiente y seleccionar la noche como momento mas propicio para oír mis podcast.
Sin embargo hoy voy a hablar de un tema que va a requerir, al menos echarle un vistazo a la web para ver un mandala y las definiciones geométricas y numéricas que voy a dar. Dicho esto, tampoco pasa nada si se oye el podcast, puesto que pasaré resumidamente por esas parte y me centraré en las ideas esenciales que pueden ser descritas con la palabra mas que con los números.
He descubierto que colorear mandalas es una actividad relajante y placentera y no solo eso. Os aseguro que abre puertas mentales, es como un nuevo estado alterado de conciencia. Anoche estuve haciendo el que podéis ver en la imagen principal, intentando combinar siempre el mismo conjunto de colores, ir alternándolos, en fin, la técnica no es muy complicada y el resultado puede ser espectacular.
Me llevó cerca de dos horas terminarlo, pero transcurrido ese tiempo mi mente se había expandido. La manera de colorear un mandala es bien simple. Se imprime el diseño en una buena impresora, se toma una caja con muchos rotuladores da varias gamas cromáticas y se procede al coloreado.
Es la mejor opción para incrementar el número de conexiones cerebrales al tener que coordinar vista, mano y cerebro, tener destreza en rellenar los huecos de manera uniforme, etc. Yo lo he intentado y francamente no me gusta mucho el resultado. Primero porque muchas veces los rotuladores no son adecuados, no se parece el color que deja en el papel con el que dice tener el propio rotulador.
Además el rellenado no es perfecto, el papel se humedece mucho…en fin, creo que hay que practicarlo, pero con diseños complejos como el de la figura, puede convertirse en una labor pesada aunque gratificante.
Y he optado por usar un artilugio electrónico. Una tablet samsung de esas que vienen con un pen electrónico. Existe una infinidad de mandalas en blanco y es cuestión de rellenar los huecos con el pen. Tienen la ventaja de que una vez hecho, el resultado es perfecto, no existen marcas de trazado, el coloreado es liso y sin borrones o inhomogeneidades. Además se puede imprimir las veces que se quiera.
DEFINICIÓN DE MANDALA
Bueno, pues tras este rollo introductorio, me interesó bastante el tema y anduve buscando información sobre los mandalas, su origen etc. No gran cosa, porque yo solo quería fijar algunas ideas. Como pasa en muchas otras ocasiones, la búsqueda por internet fue frustrante. Definiciones absurdas y lugares comunes en diversos blogs y páginas web que además estaban copiados unos de otros.
Si algún día se quitara la información redundante de internet, se reduciría a un cuarto de su tamaño.
No me gustaron las definiciones que encontré, y voy a dar mi definición formal.
Los mandalas se basan en el concepto geométrico de círculos concéntricos. No hay que ser doctor en matemáticas para saber lo que son unos círculos concéntricos. Es un concepto simple
Entonces tenemos que un mandala se construye tomando un punto en el plano que será el centro del círculo contenedor del mandala.
Con centro en ese punto vamos trazando sucesivos círculos de radios:
r1, r2,…rn
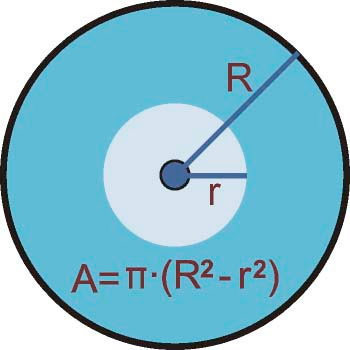
Esos n radios definen n coronas circulares siendo R=rn el radio exterior de la última corona que coincide con R, el radio del círculo contenedor del mandala.
En fin, observando la figura se pueden deducir las áreas de las sucesivas coronas, las proporciones, etc. Eso no nos interesa. Con lo que tenemos que quedarnos es que el mandala está contenido en un círculo contenedor que está dividido en coronas n circulares y que casa una de ellas contiene una parte del mandala.
¿Y que tienen exactamente esas n coronas circulares?, pues una parte del diseño del mandala, que no es otra cosa que una intrincada sucesión de curvas planas que de alguna manera rellenan cada corona circular. Estas curvas cortan a los bordes de la corona en varios puntos y las curvas de la siguiente corona conectan con estos puntos por abajo y por arriba y así sucesivamente.
En la última corona, la mas exterior, ya no hay mas figuras con las que conectar, luego las terminaciones exteriores son tangentes al círculo mas externo.
Luego vemos que un mandala tiene n parámetros básicos que son los n radios concéntricos. y dentro de los espacios circulares definidos por esos radios tenemos determinados diseños. Bien, como vemos no es tan difícil matematizar un objeto, dándole una definición que al menos, aspire a ser lo mas rigurosa posible.
RELACIÓN DE LOS MANDALAS CON LOS FRACTALES
Anoche, dándole vueltas a esto, me fijé que en google había gente que había hecho esa consulta. ¿Qué relación existe entre mandalas y fractales?. Picado por la curiosidad entré en alguna página o blog que se animaba a atacar el problema, pero la verdad es que no vi nada interesante, mas allá de definir ambas cosas pero sin abordar relaciones de semejanza alguna. Por no hablar de alguna tontería que otra.
Como el tema me interesaba, pensé que igual dándole al coco se podría hallar alguna relación entre mandalas y fractales, y vaya si la hay. Por lo menos yo creo haber hallado una. Creo que el haber hecho uno las dos horas anteriores predispuso mi mente para pensar con eficacia en el asunto.
Veréis, un fractal es un objeto de dimensión fraccionaria. Caben mas caraterísticas en la definición, pero de momento nos quedaremos con esta. Hay muchos objetos fractales, pero vamos a fijarnos en uno muy simpleç: La curva de Koch:
También podremos decir de la curva de Koch que:
- es un objeto autosimilar
- se crea por un proceso iterativo
- no es una curva diferenciable, o sea no se puede trazar tangente en ninguno de sus puntos.
- encierra un área finita
- si la cortamos y la estiramos tendríamos una recta de longitud infinita.
Todas estas características nos llevan a una definición rigurosa de la dimensión topológica de la curva de Koch, que sale de un razonamiento y unos cálculos que la verdad es que no son complicados, pero que excede un poco de lo que yo quiero contar aquí. Solo diremos que su dimensión topológica es de 1,26.
Este es un resultado asombroso. Siendo una línea su dimensión debería de ser 1, sin embargo está entre 1 y 2. ¿Qué nos quiere decir esto?, y aquí está la madre del cordero. Pues que un fractal, de alguna manera rellena mas el plano que una curva normal. Esto que puede parecer difícil de ver, lo vais a captar en seguida con un ejemplo. Si yo divido un cuadrado en cuadritos como un tablero de ajedrez, las rayas pueden ser mas o menos gruesas, pero siempre puedo hacerlas todo lo finas que yo quiera y el tablero de ajedrez se sigue viendo. No veríamos las rayas, pero veríamos las casillas con un borde invisible.
Nuestro cerebro rellenaría ese borde inexistente. Pero eso no sucede así con los objetos fractales. Si hago mas delgadas las líneas, la curva desaparece y mi cerebro no es capaz de diferenciar las regiones que separa, porque sería un proceso con infinitos pasos. Lo cual quiere decir, que la curva está cubriendo mas área dentro del plano de dibujo.
Esto nos lleva a mi invento de ayer por la noche. Si el fractal, de alguna manera imaginativa, pudiera asimilarse a un mandala para colorear, deberemos asumir que no toda la superficie del papel de dibujo está disponible para colorear. Es lo que yo he llamado dimensión de teselado o de coloreado. Vendría a ser la diferencia entre 2 que es la dimensión del papel y la parte fraccionaria de la dimensión topológica del fractal. Es decir, digámoslo así «lo que nos deja libre el trazado del fractal para colorear o dibujar otras cosas.
Dimensión de teselado = 2 – Parte fraccionaria de dimensión fractal
Para el caso de la curva de Koch sería:
Dimensión de teselado = 2 – 0,26 =1,74
Esto sería lo máximo que podríamos aprovechar de la hoja de dibujo para colorear.
Bueno, todo esto está muy bien pero ¿qué relacion tiene un mandala con un fractal?. Yo lo veo muy simple. Fijaros en la curva de Koch. Se construye con proceso iterativo, donde cada iteración afina un poco mas la geometría de la curva, pero realmente es un proceso que no tiene fin. Existen infinitas iteraciones. Por eso los fractales no pueden dibujarse. Las figuras fantásticas que hacen cierto software no son mas que el máximo de iteraciones que permite la tarjeta gráfica del equipo.
Los fractales no pueden crearse en este universo. Son una construcción de la mente humana. Necesitan de infinitos pasos, que es imposible llevarlos a cabo en el mundo físico, en este cosmos material.
Esta idea ha de quedar clara, un fractal es un objeto que requiere infinitos pasos para ser construido. Y aquí viene la relación con los mandalas. Un mandala vendría a ser un fractal que no completa su construcción por requerir infinitos pasos, y que se queda digamos en los 10, 15, 20 primeros pasos de la construcción. Es pues un fractal en potencia y la magia y la vistosidad del mandala se debe al fractal lejano que hay en su interior.
Es un atisbo de un espacio infinito dentro de otro finito, y son muy propicios para entrar en un estado alterado de conciencia tanto en su coloreado como en la contemplación. Viendo las volutas y diseños de los mandalas es fácil imaginar que se duplican, triplican y se multiplican hasta el infinito, pero sin salirse del corto espacio de dibujo. En el fondo es como abrir una puerta dimensional. Para entender como son las otras dimensiones, existen muchos símiles geométricos que podemos utilizar.
Pero para intentar «ver» las otras dimensiones, accedemos a una imposibilidad conceptual, que solo puede ser superada por un esfuerzo mental de concentración en determinados diagramas como por ejemplo los mandalas. Así hacía el protagonista del cuento: los perros de Tíndalos publicado en esta misma web.
Se me ocurre que la visualización de determinados mandalas puede servir de ayuda para evocar a los muertos en una sesión de cataptromancia y así propiciar la aparición de entidades al otro lado del espejo. Sin duda es un tema de misterio apasionante y cuesta creer la pobreza de conceptos y desarrollo que hay en la web cuando buscas información. En fin, no hay nada como pensar, que es gratis, y tener ideas propias originales. Luego serán incompletas, estaránn algo equivocadas o ya se le habrán ocurrido a otros antes que a ti, pero es un ejercicio que hay que hacer siempre.