Cálculo de la Pirámide esférica

Planteamiento y resolución de un problema de geometría sagrada

El nombre de geometría sagrada data de la época faraónica para referirse al arte de crear obras bellas y armónicas aplicando la geometría al arte. Se creó así un arte sagrado, enfocado hacia el arte real y religiosos. Trabajaron con leyes y métodos que han sobrevivido hasta nuestros días.

Esto que acabo de decir y que viene en un libro que me han regalado por el día del padre, podría ser una buena definición de lo que es la geometría sagrada. Escribo apresuradamente este post, porque después de estar dos días peleándome con un complicado problema con las pirámides, por fin he encontrado una solución simple y elegante para un problema que me ha levantado un buen dolor de cabeza.

Debo decir que este post tiene como dos partes. La primera de ellas se puede leer y escuchar el el podcast correspondiente como siempre hago. Pero la siguiente parte, forzosamente no puede ir hablada porque es el planteamiento y la resolución del problema, y lo que hay son pues cálculo, ecuaciones, gráficos y esas cosas, que hay que verlas en la web y no es posible hablarlas. Pero no obstante, antes de llegar a esa parte voy a hacer una introducción extensa y ya veréis como se capta bien lo que quiero decir.

La geometría sagrada yo la considero una parte del misterio. Realmente no es difícil aprenderla. En la mayor parte de los casos se trataría de medir las magnitudes principales de edificios, monumentos, pinturas, esculturas, etc y se trataría de:

1. Asignar determinados significados esotéricos a esas magnitudes geométricas
2. Encontrar relaciones numéricas simples entre esas magnitudes y determinados números como phi o pi o la base de los logaritmos neperianos por ejemplo.

Veamos un caso. Si tomamos una pirámide de base cuadrada, dicha base representa al mundo material donde habitan los hombres, y la cúspide de la pirámide que se eleva a través de las caras, sería ese camino de elevación que tiene que seguir la humanidad para encontrarse con los dioses. Así pues la pirámide como elemento de geometría sagrada tendría un significado de elevación de lo material a lo espiritual.

Veremos que de las infinitas pirámides que los egipcios pudieron construir, solo levantaron aquellas cuya geometría expresaba una propiedad matemática o mitológica. Podríamos preguntarnos si cada pirámide expresa un atributo divino o una relación entre la tierra y el cielo, o entre el hombre y los dioses, entonces ¿las propiedades geométricas de las pirámides expresaban ese mismo atributo o relación?.

Al final resulta sorprendente la cantidad de relaciones matemáticas concretas que existen por ejemplo entre las magnitudes de las pirámides, pero también con otras obras de arte. Hay infinidad de libros sobre geometría sagrada donde se pueden estudiar todas esas relaciones geométricas y aritméticas. Hoy mismo antes de escribir este post, he añadido un texto sobre geometría sagrada en la biblioteca de esta Cripta.

Y siempre he tenido el interés de añadir algún desarrollo propio a este tema. Algo origina, o al menos, si no es original, pues resuelto y presentado de manera novedosa. Pienso en este sentido, que en una pirámide de base cuadrada como lo son las pirámides egipcias, hay dos parámetros que la definen perfectamente mucho mejor que la altura. Esos parámetros serían el lado del cuadrado de la base y sobre todo, el ángulo de inclinación hacia el eje de las caras. El lado nos da la dimensión básica de la pirámide. Nos dice lo grande que va a ser. En la pirámide de Keops, ese lado si no recuerdo mal es de 230 metros, casi un cuarto de kilómetro. Dar cuatro vueltas a la pirámide se tardaría una hora a buen paso. Ese lado de 230 metros nos está diciendo que estamos ante una construcción enorme.

Pero el ángulo de inclinación de las caras nos dice mucho mas. Nos dice cuánto se eleva la pirámide hacia el cielo. En el caso de la pirámide de Keops estamos hablando de 53 grados, que es bastante. Es una pendiente muy pronunciada, nos está diciendo que esa pirámide con esa base alcanzará una enorme altura. De hecho, la pirámide de Keops fue el edificio mas alto del mundo durante 45 siglos! hasta que se construyó la torre Eiffel. Tengo un post donde hablo largo y tendido de las dimensiones de la gran pirámide de Keops. Se puede consultar aquí. La pirámide de Keops mide nada menos que 146 metros de altura.

La verdad es que pensar que una civilización como la egipcia cuyos conocimientos matemáticos se limitaban a dibujar rayas en la arena y contar con palitroques, pudiera hacer esas magnas obras con ridículas herramientas de cobre, se hace difícil de digerir. Pero bueno, no es momento de hablar de ese tema. Los expertos dicen que fue todo a base de fuerza muscular y mucho ojo de buen cubero.

Pues pensaba yo hace dos días cuál sería mi aportación a la geometría sagrada y pensé en lo siguiente. Todos sabemos que la esfera es un sólido perfecto, sagrado con evidentes connotaciones divinas y que tiene la propiedad de encerrar el mayor volumen en la menor superficie, por eso muchos depósitos son esféricos entre otras cuestiones. Para ahorrar material.

Pensé entonces en encontrar una pirámide esférica. Es decir una pirámide que para una superficie dada tuviera volumen máximo. Dicho de otra forma, si yo digo que la superficie de una pirámide es digamos de 3 en las unidades que sea, eso me da igual, está claro que hay infinitas pirámides de superficie 3. Bien pues se trataría de, jugando a variar el lado y el ángulo de inclinación, hallar la que tuviera un volumen máximo. Ya os adelanto que solo hay una que tiene volumen máximo.

Empecé a resolver el problema intentando encontrar una solución sencilla y accesible para poder publicarla en esta Cripta. Fueron vanos los intentos, el problema se retorcía y se complicaba y salín unos cálculo farragosos. Ya un poco mosqueado, recurrí a Google a ver si alguien lo había resuelto. No niego que un problema tan conocido como este no se haya resuelto una y mil veces. Pero yo no encontré ninguna solución en internet. Seguro que la hay. No digo que no. Solo digo que yo no la encontré. Había problemas parecidos resueltos, pero este en concreto no.

Bueno, pues opté por una solución usando los multiplicadores de Lagrange y toda la parafernalia del cálculo, pero esa solución no se puede publicar porque es muy compleja y además salían unas ristras de expresiones algebraicas interminables . Y hoy después de 24 horas infructuosas he dado con una solución que a mi me parece simple, muy gráfica, que todo el mundo va a ver y que tiene una explicación a la vez geométrica y analítica.

La demostración está al final del post. Yo solo voy a deciros ahora el resultado final. 63 grados. Esa es la inclinación que tiene que tener una pirámide de base cuadrada para que dada una superficie constante su volumen sea máximo. Es decir que tenga la misma propiedad que una esfera. De ahí el nombre que le he dado de pirámide esférica. Sin embargo sólo una pirámide en Egipto tiene una inclinación de 60 grados 3 menos que la pirámide esférica.

Las pirámides de Keops, Kefrén y Micerinos, pertenecen a un mismo tipo, que incluyen una estructura llamada triángulo de Keops o de Kepler y en su diseño se hace hincapié en la relación de sus dimensiones con el número áureo. Si la pirámide de Keops hubiera sido una pirámide esférica de 230 metros de lado, hubiera alcanzado la colosal altura de 225 metros. Hubiera encerrado mucho mas volumen usando no demasiados sillares mas para su construcción.

Una pirámide esférica sería ciertamente grandiosa y el sólo hecho de contemplarla nos introduciría en el misterio de su dimensionalidad. Por dentro, una pirámide de ese tamaño daría vértigo mirarla si estuviera hueca, pero todo ese inmenso espacio termina en un solo punto o pico agudo que es el vértice. Supuestamente la parte divina de la construcción. Veríamos aquí que para acceder a la divinidad tenemos que pasar por un único punto. Nada material puede pasar por un único punto, luego para acceder a la divinidad tenemos de des-materializarnos y convertirnos en espíritu. Ya dijo el propio Jesucristo que se entra al cielo por una puerta muy estrecha, o sea la cúspide de la pirámide. Y se entra al infierno por una puerta grande y espaciosa, la base de la pirámide.

De hecho en la base de la pirámide de Keops hay un pasadizo y un pozo que descienden hasta un recinto subterráneo. Para mí eso representa el descenso al inframundo, al infierno, a algo mas denso y oscuro que la propia materia representada por el cuadrado base de la pirámide. Es decir que cuando el faraón muere, la pirámide hace de una especie de «nave espiritual» que lo transporta al mas allá a través de la cúspide. Pero también existe la posibilidad de descender ad ínferos.

De hecho en la pirámide de Keops existe un sarcófago pero no se ha encontrado nunca una momia. Según los expertos cuando el faraón muere se usa la pirámide para una especie de ceremonia funeraria donde se le deja en el sarcófago y luego se le saca. Bien pudiera ser para que su alma escape por la cúspide de la pirámide dejando la momia como simple materia inerte. 

Cálculo del grado de inclinación

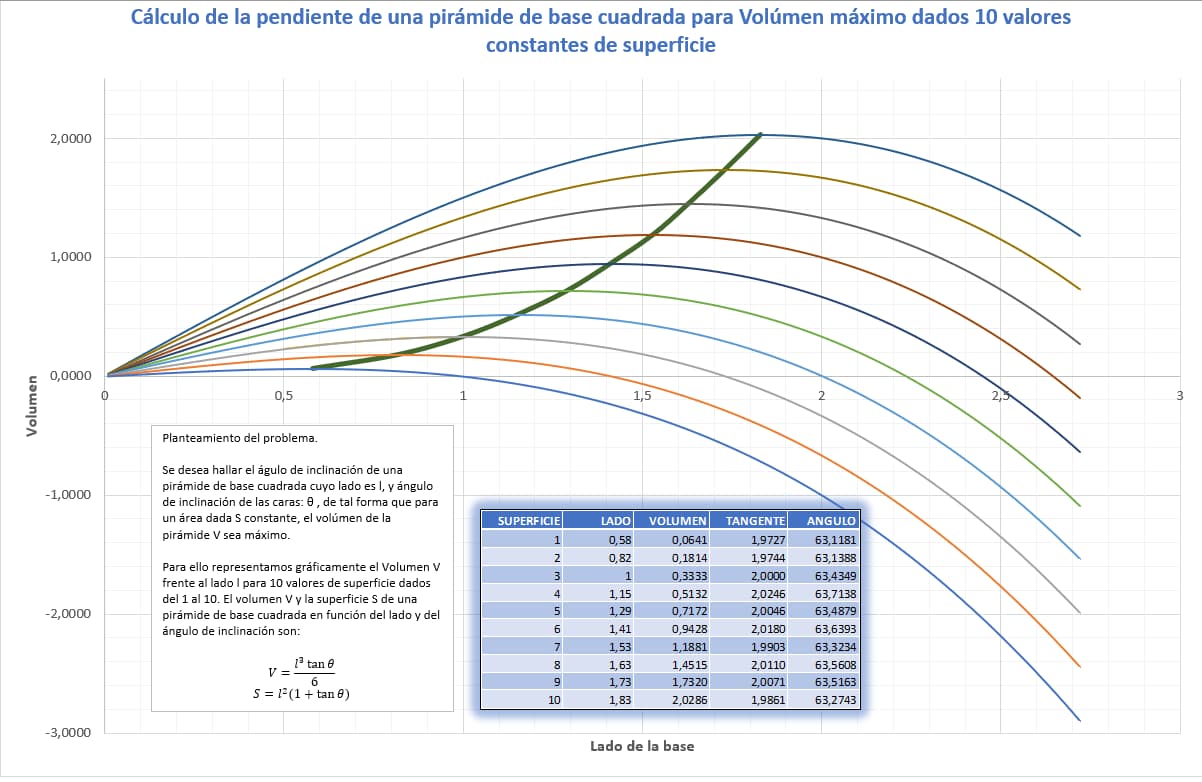
Planteamiento del problema.

Se desea hallar el ángulo de inclinación de una pirámide de base cuadrada cuyo lado es l, y ángulo de inclinación de las caras: θ , de tal forma que para un área dada S constante, el volumen de la pirámide V sea máximo.

Para ello representamos gráficamente el Volumen V frente al lado l para 10 valores de superficie dados del 1 al 10. El volumen V y la superficie S de una pirámide de base cuadrada en función del lado y del ángulo de inclinación son:

V=(l^3  tan⁡θ)/6

S=l^2 (1+tan⁡θ )

Hacemos una tabla de valores en las que hacemos variar S de 1 a 10

Calculamos para cada uno de esos valores de S, el volumen, haciendo variar S

Representamos gráficamente cada grupo de esos valores. Eso nos da el volumen máximo buscado para cada superficie.

Calculamos el ángulo de inclinación para cada volumen máximo y el valor de lado correspondiente.

Observamos que para los 10 valores propuestos de superficie, el ángulo de inclinación a volumen máximo es el mismo: 63 grados en números redondos.

Trazamos la gráfica número 11 representando lado de los máximos frente a volumen y observamos que  esa curva corta a las 10 gráficas justo en los máximos, lo cual cierra el problema.

La hoja de Excel con los cálculos y los datos se puede descargar aquí.