Esto es un problema curioso. Tenemos el conjunto de los números enteros. Dicho conjunto es infinito numerable, es decir tiene un grado de infinitud Aleph-cero. Porque no todos los infinitos son igual de infinitos. Hay unos que son mas grandes que otros, aunque parezca mentira.
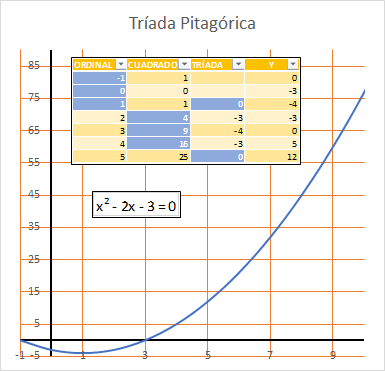
Bien, se trata de tomar 3 números cualesquiera consecutivos y verificar que la suma del los cuadrados de los dos mas pequeños es igual al cuadrado del mas grande.
Dicho trío de números, existan los que existan son singulares por ser consecutivos, pero también por cumplir el teorema de Pitágoras. De ahí el bautismo que reciben de tríadas pitagóricas.
Es fácil ver la primera. Todo el mundo conoce que:
3×3 + 4×4 = 5×5
es decir, la suma de los cuadrados de 3 y 4 es igual al cuadrado de 5. es decir, los enteros consecutivos 3,4,5 están conectados en una llamada tríada pitagórica.
Nos preguntamos si es la única terna de enteros que cumple esto o habría mas. Es un teorema fácil que ya está demostrado, pero yo he hallado otra posible demostración (aunque seguro que no he sido el único).
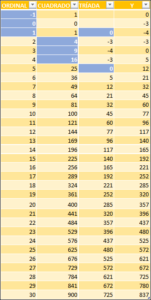
Lo demostramos calculando para cada entero su cuadrado. Luego para cada 2 consecutivos calculamos la suma. Luego ajustamos una curva que pase por todos esos puntos.
Esa curva resulta ser una ecuación de segundo grado que se cumple solo para la terna del enunciado, según se ve en las imágenes adjuntas.
Bueno, esto no es del todo cierto. Como toda ecuación de segundo grado tiene 2 soluciones. Una da ellas da como resultado la tríada (3,4,5) pero existe otra tríada (-1,0,1). Alguien podría decir que no hay una solución sino dos.
Pero esto no es así. -1 no pertenece al conjunto de los números naturales, y hay controversia sobre si el 0 debería o no ser incluído. Así que sólo existe una solución entre todos los infinitos números naturales.
Aquí se puede descargar una hoja de cálculo donde dejo a la vista las fórmulas.